ZLOMKY
Dělení dvou celých čísel a : b (b ≠ 0) můžeme psát ve tvaru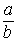 
, který se nazývá zlomek, vodorovná čárka je zlomková čára, číslo a čitatel a číslo b jmenovatel zlomku.
Porovnání zlomku podle velikosti. Znásobíme-li čitatele prvního zlomku jmenovatelem druhého zlomku a čitatele druhého zlomku jmenovatelem prvního zlomku, můžeme porovnáním součinů porovnat zlomky podle velikosti na základě těchto zásad:
| a | x | c | Jestliže a · d = b · c, pak | a | = | c |
| b | d | b | d | |||
| a · d > b · c | a | > | c | |||
| b | d | |||||
| a · d < b · c; | a | < | c | |||
| b | d | |||||
| Příklad: | 5 | > | 3 | protože 25 > 24. |
| 8 | 5 |
Rozšiřováni zlomků. Hodnota zlomku se nezmění, znásobíme-li čitatele i jmenovatele zlomku stejným číslem různým od nuly. Této úpravě zlomku říkáme rozšiřování zlomku.
| Příklad: | a | = | a · m | = | am | 2 | = | 2 · 4 | = | 8 | |
| b | b · m | bm | 3 | 3 · 4 | 12 |
Krácení zlomků. Hodnota zlomku se nezmění, dělíme-li čitatele i jmenovatele zlomku stejným číslem různým od nuly. Této úpravě zlomku říkáme krácení zlomku.
Příklad:
| am | = | am : m | = | a | 8 | = | 8 : 4 | = | 2 | |
| bm | bm : m | b | 12 | 12 : 4 | 3 |
Sčítání (odčítání) zlomků. Zlomky se stejnými jmenovateli sečteme (odečteme), lomíme-li součet (rozdíl) čitatelů společným jmenovatelem. Zlomky s různými jmenovateli sečteme, převedemi-li zlomky na společného jmenovatele vhodným rozšířením.
Příklad:
| a | + | b | = | a + b | 1 | + | 3 | = | 4 | |
| m | m | m | 5 | 5 | 5 |
| a | + | b | = | an | + | bm | = | an + bm |
| m | n | mn | nm | mn |
| 2 | + | 3 | = | 8 | + | 9 | = | 17 |
| 3 | 4 | 12 | 12 | 12 |
Násobení zlomků. Zlomek násobíme zlomkem, lomíme-li součin čitatelů součinem jmenovatelů.
Příklad:
| a | · | m | = | am | 2 | · | 3 | = | 2 · 3 | = | 6 | = | 1 | |
| b | n | bn | 3 | 4 | 3 · 4 | 12 | 2 |
Dělení zlomků. Zlomek dělíme zlomkem, násobíme-li dělence převráceným zlomkem dělitele.
Příklad:
| a | : | m | = | a | · | n | = | an |
| b | n | b | m | bm |
| 2 | : | 3 | = | 2 | · | 7 | = | 14 |
| 5 | 7 | 5 | 3 | 15 |
Desetinný rozvoj. Každé reálné číslo lze napsat desetinným rozvojem, který může být ukončený (například 1/2 = 0,5) nebo neukončený (nekonečný), přičemž rozeznáváme
- periodický desetinný rozvoj, v němž se od určitého místa jedna z číslic nebo skupina číslic pravidelně opakuje, například
1 = 0,3333 . . . = 0,3 3 1 = 0,0909 . . . = 0,09 11 1 = 0,1666 . . . = 0,16 6 3 = 0,428571 . . . = 0,428571 7 - neperiodický desetinný rozvoj, v němž se sled číslic za desetinnou čárkou nikdy pravidelně neopakuje, například
√2 = 1,414213 . . . π = 3,141592 . . .
Číslo 0.16 čteme „nula celá jedna desetina šest periodických“, číslo 1 se nazývá předperioda, číslo 6 perioda. Číslo 0,16 se nazývá číslo neryze periodické, na rozdíl od čísla 0,09, které se nazývá číslo ryze periodické (perioda následuje ihned za desetinnou čárkou).
Zaokrouhlování čísel. Čísla zaokrouhlujeme na určitý počet platných číslic podle těchto pravidel:
Je-li první zanedbaná číslice
číslice menší než 5, pak poslední platnou číslici ponecháme beze změny, například
2,34 = 2,3 2635 = 2600
číslice větší než 5, pak poslední platnou číslici zvětšíme o jednotku, například
2,36 ± 2,4 2675 ± 2700
číslice 5 a za ní následuje alespoň jedna číslice různá od nuly, pak poslední platnou číslici zvětšíme o jednotku, například
2,351=2,4 2651=2700
číslice 5 a za ní následují samé nuly, pak zaokrouhlujeme tak, aby byla poslední platná číslice vždy sudá, například
2,350 = 2,4 2,650=2,6