ROVINNÝ ÚHEL
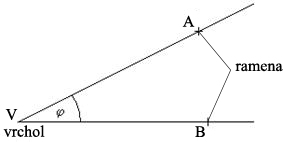
Úhel AVB je část roviny (obrázek), ohraničená dvojicí polopřímek VA, VB se společným počátkem V. Polopřímky VA, VB se nazývají ramena úhlu, bod V vrchol úhlu.
Velikost úhlu měříme obvykle ve stupních.
Úhel tvořený dvěma navzájem opačnými po lopřímkami se nazývá přímý úhel a má velikost ve stupních α = 180°. Sto osmdesátá část velikosti přímého úhlu má velikost jednoho úhlového stupně s označením 1°. Menšími úhlovými jednotkami jsou úhlová minuta 1' a úhlová vteřina 1", přičemž platí
1° = 60' 1' = 60" 1° = 3600"
V Mezinárodní soustavě jednotek SI je jednotkou rovinného úhlu radián s označením rad, přičemž platí
| 1° = | π | rad |
| 180 |
Při převádění úhlových stupňů na radiány a naopak používáme trojčlenky
| ↑ | π 1 ° · · · · · · · · · · · · · · · · · 180 |
↑ |
| x ° . . . . . . . . . . . . . . . . y rad |
z níž například vyplývá
| 90° = | π | rad |
| 2 |
180° = π rad
360° = 2π rad
Velikost pravého úhlu 90° se označuje R. Při převádění úhlových stupňů na díly nebo násobky R a naopak používáme trojčlenky
| ↑ | 90° . . . . . . . . . . . . . . . . . 1 R | ↑ |
| x° . . . . . . . . . . . . . . . . . . y R |
z níž například vyplývá
| 1 | R = | 1 | · 90° = 45° |
| 2 | 2 |
| 30° = | 30° | R = | 1 | R |
| 90° | 3 |
2R = 2 · 90° = 180°
Rozdělení úhlů podle velikosti je znázorněno na obrázku. Úhly 0° ≦ a ≦ 180° se nazývají konvexní úhly, úhly velikosti 180° < α < 360° nekonvexní úhly. Úhly ostré a tupé se nazývají úhly kosé.

α = 0° |
0° < α < 90° |
 α = 90° |
90° < α < 180° |
α = 180° |

180° < α < 360° |
α = 360°
plný