MOCNINY A ODMOCNINY
Mocniny
Mocnina ab, kde a ≥ 0 a b je přirozené číslo, vyjadřuje součin b činitelů čísla a.
Příklad: a2 = a · a 34 = 3 · 3 · 3 · 3
Číslo a se nazývá základ mocniny, číslo b mocnitel (exponent), početní výkon umocňování. Mocninu 32 čteme „tři na druhou“, mocninu ab čteme „a na b-tou“ nebo „b-tá mocnina a“.
Pro b = 0 a b = 1 platí
a0 = 1 30 = 1
a1 = a 31 = 3
Každou mocninu můžeme vypočítat tak, že základ a znásobíme mezi sebou tolikrát, kolikrát dává mocnitel b.
Příklad:
32 = 3 · 3 = 9
24 = 2 · 2 · 2 · 2 = 16
Druhé a třetí mocniny čísel 1 až 10 a některých dalších čísel do 100 jsou uvedeny v tabulce.
|
a |
a2 |
a3 |
a |
a2 |
a3 |
|
1 |
1 |
1 |
35 |
1 225 |
42 875 |
|
2 |
4 |
8 |
40 |
1 600 |
64 000 |
|
3 |
9 |
27 |
45 |
2 025 |
91 125 |
|
4 |
16 |
64 |
50 |
2 500 |
125 000 |
|
5 |
25 |
125 |
55 |
3 025 |
166 375 |
|
6 |
36 |
216 |
60 |
3 600 |
216 000 |
|
7 |
49 |
343 |
65 |
4 225 |
274 625 |
|
8 |
64 |
512 |
70 |
4 900 |
343 000 |
|
9 |
81 |
729 |
75 |
5 625 |
421 875 |
|
10 |
100 |
1 000 |
80 |
6 400 |
512 000 |
|
15 |
225 |
3 375 |
85 |
7 225 |
614 125 |
|
20 |
400 |
8 000 |
90 |
8 100 |
729 000 |
|
25 |
625 |
15 625 |
95 |
9 025 |
857 375 |
|
30 |
900 |
27 000 |
100 |
10 000 |
1 000 000 |
Vyplývá z nich, že například
83 = 512, 453 = 91 125
Z tabulky lze určit přibližné hodnoty druhých a třetích mocnin i těch čísel, které nejsou v tabulce uvedeny.
Příklad: Hledáme-li mocninu 582, uvědomíme si, že platí
552 < 582 < 602
v tabulkách nalezneme
3 025 < 582 < 3 600
a pak odhadneme 582 = 3 400, přičemž přesně platí 582 = 3 364. Přesnou hodnotu zjistíme také pomocí vzorců pro umocňování mnohočlenů.
582 = (50 + 8)2 = 502 + 2 · 50 · 8 + 82 = 2 500 + 800 + 64 = 3 364
Odmocniny
Odmocnina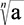 
kde a ≧ 0 a n je přirozené číslo, je nezáporné číslo q, pro něž platí qn = a.
Příklad: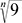 
= 3, protože 32 = 9
Číslo a se nazývá odmocněnec (základ odmocniny), číslo n odmocnitel, znak √ odmocnítko, početní výkon odmocňování. Odmocninu √9 čteme „druhá odmocnina z devíti“, odmocninu 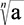čteme „n-tá odmocnina z a“. Druhé a třetí odmocniny čísel 1 až 10 a některých dalších čísel do 100 jsou uvedeny níže. Vyplývá z ní, že s přesností na tři desetinná místa například platí √8 = 2,828, ∛25 = 2,924. Ve sloupcích √10a a ∛10a nalezneme odmocniny desetinásobků čísla a, tedy například
√35 = 5,916 √350 = 18,708
∛35 = 3,271 ∛350 = 7,047
| a | √a | √10a | ∛a | ∛10a | a | √a | √10a | ∛a | ∛10a |
| 1 | 1,000 | 3,162 | 1,000 | 2,154 | 35 | 5,916 | 18,708 | 3,271 | 7,047 |
| 2 | 1,414 | 4,472 | 1,260 | 2,714 | 40 | 6,325 | 20,000 | 3,420 | 7,368 |
| 3 | 1,732 | 5,477 | 1,442 | 3,107 | 45 | 6,708 | 21,213 | 3,557 | 7,663 |
| 4 | 2,000 | 6,325 | 1,587 | 3,420 | 50 | 7,071 | 22,361 | 3,684 | 7,937 |
| 5 | 2,236 | 7,071 | 1,710 | 3,684 | 55 | 7,416 | 23,452 | 3,803 | 8,193 |
| 6 | 2,449 | 7,746 | 1,817 | 3,915 | 60 | 7,746 | 24,495 | 3,915 | 8,434 |
| 7 | 2,646 | 8,367 | 1,913 | 4,121 | 65 | 8,062 | 25,495 | 4,021 | 8,662 |
| 8 | 2,828 | 8,944 | 2,000 | 4,309 | 70 | 8,367 | 26,458 | 4,121 | 8,879 |
| 9 | 3,000 | 9,487 | 2,080 | 4,481 | 75 | 8,660 | 27,386 | 4,217 | 9,086 |
| 10 | 3,162 | 10,000 | 2,154 | 4,642 | 80 | 8,944 | 28,284 | 4,309 | 9,283 |
| 15 | 3,873 | 12,247 | 2,466 | 5,313 | 85 | 9,220 | 29,155 | 4,397 | 9,473 |
| 20 | 4,472 | 14,142 | 2,714 | 5,848 | 90 | 9,487 | 30,000 | 4,481 | 9,655 |
| 25 | 5,000 | 15,811 | 2,924 | 6,300 | 95 | 9,747 | 30,822 | 4,563 | 9,830 |
| 30 | 5,477 | 17,321 | 3,107 | 6,694 | 100 | 10,000 | 31,623 | 4,642 | 10,000 |
Podobně jako u druhých a třetích mocnin lze odhadem určit přibližné hodnoty druhých a třetích odmocnin těch čísel, která nejsou v tabulce uvedena.
Příklad: Odmocninu ∛746 odhadneme postupem
∛700 < ∛746 < ∛750
8,879 < ∛746 < 9,086
∛746 ≐ 9,07