Matematika, Fyzika, Chemie, Biologie, Zeměpis stručně

ROVNICE

Rovnice je zápis rovnosti dvou výrazů s neznámou x. V rovnici f(x) = g(x), kde f a g jsou funkce neznámé x, se výraz f(x) nazývá levá strana rovnice a výraz g(x) pravá strana rovnice. Rovnice ve tvaru f(x) - g(x) = 0 se nazývá anulovaná. Prvek x0 z definičního oboru proměnné x, který po dosazení za x změní rovnici f(x) = g(x) v rovnost f(x0) = g(x0), se nazývá kořen rovnice nebo řešení rovnice.

Příklad: Zápis 3x = x + 4 je rovnice s neznámou x. Výraz 3x se nazývá levá strana rovnice, výraz x + 4 pravá strana rovnice. Kořenem neboli řešením rovnice je číslo x0 = 2, protože po dosazení se daná rovnice změní v rovnost 3 · 2 = 2 + 4.

Podle počtu neznámých rozeznáváme rovnice s jednou, dvěma i více neznámými, napřiklad s dvěma neznámými 2x + y = 6. Podle nejvyššího mocnitele neznámé rozeznáváme rovnice prvního stupně, druhého stupně i vyšších stupňů, například rovnice druhého stupně x2 — 4x + 1 = 0 nebo třetího stupně x3 - x = 6. Podle druhu funkcí f(x), g(x) rozeznáváme mj. rovnice

algebraické: 3x = 2x + 5

exponenciální: 2x = 8

goniometrické: sin x = 1

iracionální: √2x - 1 = 3

logaritmické: log x = 2

Ekvivalentní úprava rovnice jé taková úprava, při které má původní rovnice i upravená rovnice ve stejném číselném oboru stejné kořeny. Základní ekvivalentní úpravy jsou

  • k oběma stranám rovnice můžeme přičíst (odečíst) stejné číslo (libovolný člen rovnice můžeme převést z jedné na druhou stranu rovnice se změnou znaménka)
    Příklad:
    2x - 1 = 3
    2x = 3 + 1
    2x = 4 /:2
    x = 2
  • obě strany rovnice můžeme násobit nebo dělit stejným číslem různým od nuly.

Rovnice prvního stupně neboli lineární rovnice ax + b = 0 (a ≠ 0)

  • má jediné řešení x = - Rovnice prvního stupně, jestliže a ≠ 0, b ≠ 0
  • má jediné řešení x = 0, jestliže a ≠ 0, b = 0
  • má neomezený počet řešení, jestliže se neznámá x ekvivalentními úpravami zruší a výsledkem je rovnost 0 = 0, 2 = 2 apod.
  • nemá řešení, jestliže se neznámá x ekvivalentními úpravami zruší a výsledkem je nesprávná rovnost 0 = 2 apod.

Rovnice druhého stupně neboli kvadratická rovnice má tvar ax2 + bx + c = 0, (a ≠ 0, a, b, c jsou reálná čísla). Člen ax2 se nazývá kvadratický člen, bx lineární člen a c absolutní člen.

Výraz D = b2 – 4ac se nazývá diskriminant kvadratické rovnice, jestliže

D > 0, má rovnice dva různé reálné kořeny,

D = 0, má rovnice jeden reálný kořen,

D < 0, nemá rovnice v oboru reálných čísel řešení.

Kořeny kvadratické rovnice vypočítáváme pomocí vzorce

x1,2 = - b ± √b2 - 4ac
2a

Přiklad: Rovnice x2 - 8x + 7 = 0 má dva kořeny, protože platí

D = b2 - 4ac = (—8)2 - 4 · 1 · 7 = 64 - 28 = 36 > 0

Kořeny rovnice vypočteme po dosazení do vzorce

Kořeny kvadratické rovnice

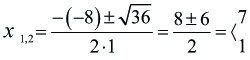
neboli x1 = 7 a x2 = 1.