ALGEBRA
Algebrou se ve školské matematice rozumí počítání s písmeny ve významu čísel.
Závorky. Pořadí početních výkonů vyznačujeme závorkami, přičemž platí úmluva, že početní výkony uzavřené v závorce provádíme nejdříve. Při sčítání a odčítání odstraňujeme závorky podle těchto pravidel:
- Je-li před závorkou znaménko + , odstraníme závorku tak, že znaménka v závorce ponecháme beze změny.
- Je-li před závorkou —, odstraníme závorku tak, že znaménka v závorce změníme v znaménka opačná.
Příklady: a + (b + c) = a + b + c a - (b + c) = a - b - c a + (b - c) = a + b - c a - (b - c) = a - b + c
Znaménka. Znaménko součinu a podílu nezáporných čísel a, b se řídí těmito pravidly:
- Součin (podíl) dvou čísel se stejnými znaménky je vždy kladný.
- Součin (podíl) dvou čísel s různými znaménky je vždy záporný.
Uvedeným pravidlům odpovídají tato schémata a příklady:
| + · + = + | (+ 3) · (+ 2) = + 6 | |
| - · - = + | (- 3) · (- 2) = + 6 | |
| + · - = - | (+ 3) · (- 2) = - 6 | |
| - · + = - | (- 3) · (+ 2) = - 6 | |
| + : + = + | (+ 6) · (+ 3) = + 2 | |
| - : - = + | (- 6) · (- 3) = + 2 | |
| + : - = - | (+ 6) · (- 3) = - 2 | |
| - : + = - | (- 6) · (+ 3) = - 2 |
Početní výkony s mocninami
Sčítání (odčítání) mocnin. Sčítat (odčítat) můžeme jen mocniny se stejným základem a stejným mocnitelem. Mocniny sečteme, sečteme-li číselné koeficienty a výsledek znásobíme společnou mocninou sčítanců.
ram + sam = (r + s)am 5a2 + 2a2 = 7a2
Násobení mocnin. Mocniny se stejným základem znásobíme, umocníme-li společný základ součtem mocnitelů.
am · an = am+n a3 . a2 = a5
Mocniny se stejným mocnitelem znásobíme, umocníme-li součin základů společným mocnitelem.
am · bm = (ab)m 22 · a2 = (2a)2
Dělení mocnin. Mocniny se stejným základem dělíme, umocníme-li společný základ rozdílem mocnitelů
| am : an = | am | = am-n (a ≠ 0) |
| an |
a5 : a3 = a2
Mocniny se stejným mocnitelem dělíme, umocníme-li podíl základů společným mocnitelem.
| am : bm = | am | = | 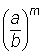
|
(b ≠ 0) |
| bm |
a3 : b3 = 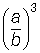
Umocňování mocnin. Mocninu umocníme, umocníme-li základ mocniny součinem mocnitelů.
(am)n = am·n (a3)2 = a6
Umocňování součinu. Součin umocníme, umocníme-li každého činitele daným mocnitelem.
(ab)m = ambm (2a)2 = 4a2
Mocniny se záporným mocnitelem. Pro každé reálné číslo a ≠ 0 a přirozené číslo n platí
| a-n = | 1 | a-3 = | 1 | |
| an | a3 | |||
| an = | 1 | a3 = | 1 | |
| a-n | a-3 |
Početní výkony s odmocninami. Pro kladné reálné číslo a, celé číslo m a přirozené číslo n platí
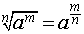
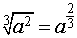
Podle této věty můžeme převést odmocniny na mocniny s mocniteli ve tvaru zlomku a s nimi počítat podle pravidel o počítání s mocninami a zlomky, jak vyplývá z těchto příkladů:
Krácení odmocnin 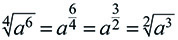
Násobení odmocnin 
Odmocňování odmocnin
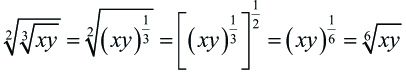
Mnohočleny
Násobení
(a + b) · m = am + bm
(a + b) · (m + n ) = am + bm + an + bn
(a + b) · (a + b) = a2 + 2ab + b2
(a - b) · (a - b) = a2 - 2ab - b2
(a + b) · (a - b) = a2 - b2
Dělení
| (a + b) : m = | a | + | b |
| m | m |
(a2 + 2ab + b2) : (a + b) = a + b
(a2 - 2ab + b2) : (a - b) = a - b
(a2 - b2) : (a + b) = a - b
(a2 - b2) : (a - b) = a + b
(a3 + b3) : (a + b) = a2 - ab + b2
(a3 - b3) : (a - b) = a2 + ab + b2
Umocňování
(a + b)2 = a2 + 2ab + b2
(a — b)2 = a2 — 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a — b)3 = a3 — 3a2b + 3ab2 — b3
Rozklad
a2 - b2 = (a + b) · (a - b)
a2 + 2ab + b2 = (a + b) · (a + b)
a2 - 2ab + b2 = (a - b) · (a - b)