OBVODY A OBSAHY
Obvod označujeme písmenem o, obsah písmenem S. Označení prvků jednotlivých geometrických útvarů je zřejmé z připojených nákresů.
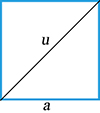
Čtverec:
| o = 4a S= a2 S = | 1 | u2 |
| 2 |
u = a√2 ≐ 1,414a
| a = | √2 | u ≐ 0,707u |
| 2 |
Obdélník:
o = 2(a + b) S = ab

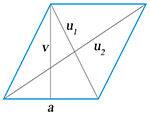
Kosočtverec:
| o = 4a S = av S = | 1 | u1u2 |
| 2 |
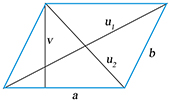
Rovnoběžník:

Trojúhelník:
| o = a + b + c S = | 1 | av |
| 2 |
| S = | 1 | r(a + b + c) |
| 2 |
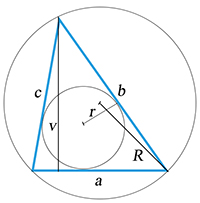
| S = | abc |
| 4R |
S = √s(s –a) (s – b) (s – c)
| s = | 1 | (a + b+ c) |
| 2 |
R - poloměr kružnice opsané
r - poloměr kružnice vepsané
Trojúhelník pravoúhlý:
| s = | 1 | ab |
| 2 |
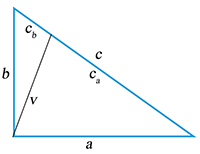
Pythagorova věta
a2 + b2 = c2
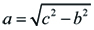
Euklidovy věty
v2 = cacb a2 = cac b2 = cbc
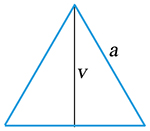
Trojúhelník rovnostranný:
| S = | a2 | √3 ≐0,433a2 |
| 4 |
S ≐ 0,577v2
v ≐ 0,866a
a ≐ 1,155v
Lichoběžník:
o = a + b + c + d
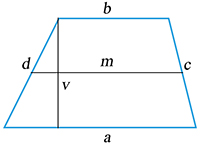
| S = | 1 | (a + b)v |
| 2 |
| S = mv m = | 1 | (a + b) |
| 2 |
m — střední příčka
Pravidelný mnohoúhelník:
o = na
| S = | 1 | nar |
| 2 |
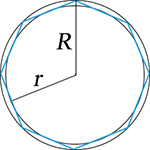
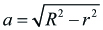
n – počet stran
r – poloměr kružnice vepsané
R – poloměr kružnice opsané
Kružnice, kruh:
o = 2πr o = πd o = 2√πS
| S = πr2 S = | πd2 | S = | od |
| 4 | 4 |
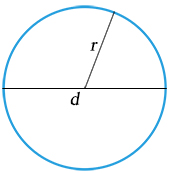
π ≐ 3,141592 . . .
| r = | o | ≐ 0,159o |
| 2π |
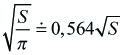
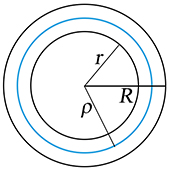
Mezikruží:
S = π(R2 – r2) S = 2πρσ
| ρ = | R + r | σ = R – r |
| 2 |