TROJÚHELNÍKY
Podle velikosti úhlů rozeznáváme trojúhelníky (viz tabulka)
- ostroúhlé, jejichž všechny vnitřní úhly jsou ostré
- pravoúhlé, jejichž jeden vnitřní úhel je pravý
- tupoúhlé, jejichž jeden vnitřní úhel je tupý.
Podle velikosti stran rozeznáváme trojúhelníky
- různoramenné, jejichž žádné dvě strany nejsou shodné
- rovnoramenné, jejichž právě dvě strany jsou shodné
- rovnostranné, jejichž všechny strany jsou shodné.
| trojúhelník | různoramenný | rovnoramenný | rovnostranný |
| ostroúhlý |
|
||
| pravoúhlý | |||
| tupoúhlý |
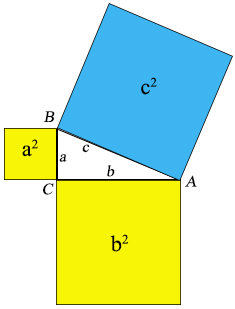
Pythagorova věta
Obsah čtverce sestrojeného nad přeponou pravoúhlého trojúhelníku se rovná součtu obsahů čtverců sestrojených nad jeho odvěsnami. Jsou-li v pravoúhlém trojúhelníku a, b velikosti odvěsen a c velikost přepony, platí
c2 = a2 + b2
Euklidova věta o odvěsně
Obsah čtverce sestrojeného nad odvěsnou pravoúhlého trojúhelníku je roven obsahu obdélníku sestrojeného z přepony a úseku na přeponě k odvěsně přilehlého. Jsou-li a, c, ca velikosti příslušných úseček v pravoúhlém trojúhelníku, platí
a2 = c · ca

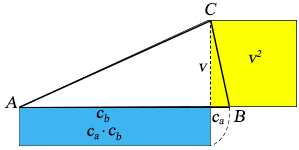
Euklidova věta o výšce
Obsah čtverce sestrojeného nad výškou pravoúhlého trojúhelníku je roven obsahu pravoúhelníku, jehož strany jsou úseky na přeponě k odvěsnám přilehlé. Jsou-li v, ca, cb velikosti příslušných úseček v pravoúhlém trojúhelníku, platí
v2 = ca · cb
Thaletova věta
Obvodové úhly nad průměrem kružnice jsou pravé. Thaletovy věty používáme, chceme-li z daného bodu A sestrojit k dané kružnici k tečnu t. Postupujeme takto (obrázek):
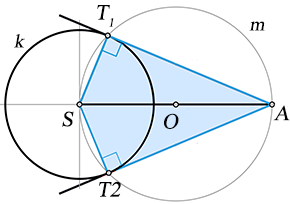
Sestrojíme úsečku SA, okolo jejího středu O opíšeme kružnici m o poloměru OA, průsečíky kružnic k, m označíme T1, T2. Přímky AT1, AT2 jsou hledané tečny.
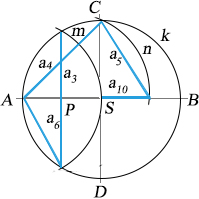
Pravidelné mnohoúhelníky
Pravidelné mnohoúhelníky jsou mnohoúhelníky, které mají všechny strany a všechny vnitřní úhly shodné. Pravidelný n-ůhelník můžeme sestrojit tak, že obvod kružnice n-úhelníku opsané rozdělíme na n stejných dílů kružítkem zkusmo, nebo u některých n-úhelníků podle nákresu na obrázku, kde AB, CD jsou kolmice procházející středem S, P je střed úsečky AS, m je oblouk kružnice opsané kolem bodu A poloměrem AS, n je oblouk kružnice opsané kolem bodu P poloměrem PC. Pravidelný pětiúhelník sestrojíme například tak, že od zvoleného bodu A přenášíme po obvodu kružnice k postupně úsečku a5, a tak určíme vrcholy pětiúhelníku ABCDE.
Trigonometrie
Trigonometrie pravoúhlého trojúhelníku se zabývá vztahy mezi jeho stranami a úhly. V pravoúhlém trojúhelníku ABC (obrázek),
| sin α = | a | cos α = | b | tg α = | a |
| c | c | b |

kde například stranu a nazýváme protilehlá odvěsna k úhlu α, lze určit šest goniometrických funkcí ostrého úhlu, z nichž nejdůležitější tři definujeme podle obrázku. Hodnoty goniometrických funkcí ostrého úhlu α zaokrouhlené na dvě desetinná místa jsou uvedeny v tabulce (funkce tg 90° není definována).
|
α° |
sin α |
cos α |
tg α |
|
0 |
0,00 |
1,00 |
0,00 |
|
10 |
0,17 |
0,98 |
0,18 |
|
20 |
0,34 |
0,94 |
0,36 |
|
30 |
0,50 |
0,87 |
0,58 |
|
40 |
0,64 |
0,77 |
0,84 |
|
50 |
0,77 |
0,64 |
1,19 |
|
60 |
0,87 |
0,50 |
1,73 |
|
70 |
0,94 |
0,34 |
2,75 |
|
80 |
0,98 |
0,17 |
5,67 |
|
90 |
1,00 |
0,00 |
- |
Tabulky hodnot funkcí mají různé uspořádání a používáme jich podle návodu, který je k tabulkám většinou připojen. Užitím goniometrických funkcí ostrého úhlu můžeme
- vypočítat velikost ostrého úhlu pravoúhlého trojúhelníku, známe-li dvě strany trojúhelníku
- vypočítat velikost strany pravoúhlého trojúhelníku, známe-li velikost jedné strany a velikost ostrého úhlu.
- vypočítat velikost narýsovaného úhlu bez jeho měření úhloměrem
- narýsovat úhel požadované velikosti bez použití úhloměru.
Máme-li sestrojit úhel velikosti α = 40°
- nalezneme v tabulkách hodnotu goniometrické funkce tg 40° = 0,84,
- funkci tg a vyjádříme poměrem příslušných stran pravoúhlého trojúhelníku ABC a poměr vhodně zkrátíme nebo rozšíříme, tedy
tg 40° = a = 0,84 = 4,2 b 1 5 a pak a = 4,2 cm a b = 5 cm
- sestrojíme pravoúhlý trojúhelník ABC o stranách a = 4,2 cm, b = 5 cm a γ = 90°, a tím i hledaný úhel α = 40°.