MNOŽINY
Množinu si zjednodušeně představujeme jako soubor navzájem rozlišitelných objektů, z nichž lze o každém rozhodnout, zda do souboru patří nebo nepatří. Objekty, z nichž se množina skládá, se nazývají prvky. Jestliže prvek x do množinv M patří, píšeme
x ∈ M čteme „x“ je prvkem M", „prvek x patří do množiny M“ apod
Jestliže prvek x do množiny M nepatří, píšeme x ∉ M.
Množiny určujeme obvykle
- výčtem všech prvků množiny, například M = {1,2,3,4,5},
- charakteristickou vlastností všech prvků množiny, například
M = {x;x ∈ N ⋂x < 6} (množina M, jejíž prvky x jsou přirozená čísla N menší než šest, tedy množina M = {1,2,3,4,5}).
Množina, která neobsahuje žádné prvky, se nazývá prázdná množina. Prázdnou množinu zapisujeme ∅ nebo M = ∅ a čteme „množina M je prázdná“ apod.
Příklad: množina přirozených čísel menších než nula.
Konečná množina je množina, která má konečný počet prvků, tedy buď žádný prvek, nebo lze počet prvků vyjádřit přirozeným číslem nebo je počet prvků s určitostí menší než nějaké přirozené číslo.
Příklad: množina všech přirozených čísel menších než pět, množina všech druhů živočichů obývajících Zemi.
Nekonečná množina je množina, která není konečná, tedy množina, jejíž počet všech prvků nelze vyjádřit žádným přirozeným číslem.
Příklad: množina všech přirozených čísel, množina všech bodů přímky.
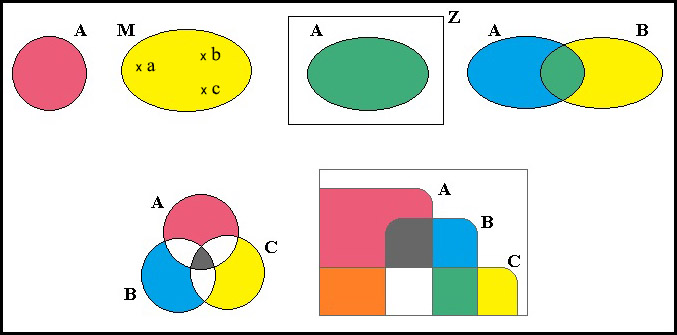
Množinové diagramy jsou grafické nákresy používané k znázorňování množin a operací s množinami. Množinové diagramy jsou tvořeny uzavřenou křivkou v rovině (kružnice, ovál, obdélník apod.), jejíž vnitřní body představují prvky množiny, jak je na několika příkladech znázorněno na obr. na této straně.
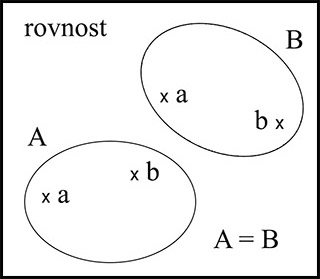
Rovnost množin. Množina A se rovná množině B, když mají obě množiny tytéž prvky (když je každý prvek množiny A prvkem množiny B a každý prvek množiny B prvkem množiny A). Rovnost množin zapisujeme
A = B čteme „A se rovná B“ nebo „A je rovna B“.
Podmnožina. Množina A je podmnožinou množiny B, je-li každý prvek množiny A také prvkem množiny B. Píšeme
A ⊂ B čteme „A je podmnožinou B“.

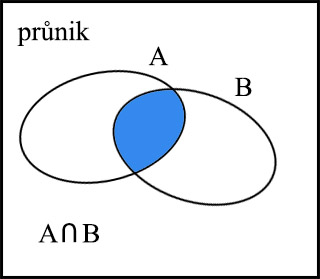
Průnik množin. Průnik množin A, B je množina všech prvků, které patří zároveň do množiny A i do množiny B. Píšeme
A ⋂ B čteme „průnik množin A a B“.
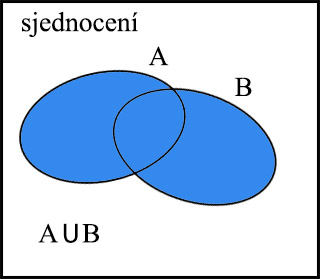
Sjednocení množin. Sjednocení množin A, B je množina všech prvků, které patří alespoň do jedné z množin A, B. Píšeme
A ⋃ B čteme „sjednocení množin A, B
Rozdíl množin. Rozdíl množin A, B je množina prvků, které jsou prvky množiny A a nejsou prvky množiny B. Píšeme
A \ B čteme „rozdíl množin A, B“.

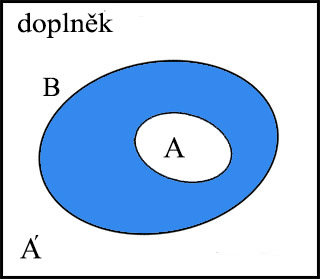
Doplněk množiny. Je-li A podmnožinou B, pak množina všech prvků B, které nejsou prvky množiny A, se nazývá doplněk množiny, přičemž platí A' = B \ A.
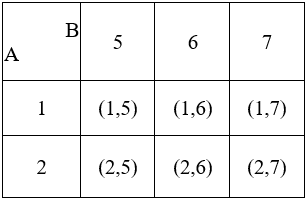
Kartézský součin. Kartézský součin množin A, B je množina všech uspořádaných dvojic (x, y), kde x je prvkem množiny A a y je prvkem množiny B. Symbol kartézského součinu A x B čteme „A krát B“.
Příklad:
A = {1,2} B = {5,6,7}
A x B = {(1,5), (1,6), (1,7), (2,5), (2,6), (2,7)}