ČÍSLA
Desítková číselná soustava
K zapisování čísel používáme znaků zvaných číslice nebo cifry. Arabské číslice 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 byly odvozeny zřejmě z indických a po Evropě se od 12. století šířily ze Španělska, kde je na školách používali Arabové.
Číselná soustava s deseti znaky se nazývá desítková nebo dekadická soustava. Deset různých číslic označuje základní jednotky neboli jednotky nultého řádu. Deset jednotek nultého řádu tvoří jednotku prvního řádu, desetina jednotky nultého řádu tvoří jednotku minus prvního řádu. Podobně se vytvářejí i jednotky vyšších a nižších řádů, jejichž názvy a zápis mocninou jsou v tabulce.
| zápis | název | řád |
| 0,000 001 | milióntiny | 10-6 |
| 0,000 01 | stotisíciny | 10-5 |
| 0,000 1 | desetitisíciny | 10-4 |
| 0,001 | tisíciny | 10-3 |
| 0,01 | setiny | 10-2 |
| 0,1 | desetiny | 10-1 |
| 1 | jednotky | 100 |
| 10 | desítky | 101 |
| 100 | sta | 102 |
| 1 000 | tisíce | 103 |
| 10 000 | desetitisíce | 104 |
| 100 000 | statisíce | 105 |
| 1 000 000 | milióny | 106 |
| 1 000 000 000 | miliardy | 109 |
| 1 000 000 000 000 | biliony | 1012 |
Dvojková číselná soustava
Počítače pracují i v jiných číselných soustavách. Například v dvojkové číselné soustavě s dvěma znaky 0 a 1. Prvních dvacet čísel desítkové soustavy se ve dvojkové soustavě zapisuje tak, jak je uvedeno v tabulce. Číslo 100 se nečte „sto“, ale „jedna nula nula“ a neznamená 100, ale 4. Podobně čteme i ostatní čísla dvojkové soustavy.
Ve dvojkové soustavě se sčítají čísla podle čtyř základních pravidel:
0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 10.
Znak 1 ve výsledném součtu poslední rovnosti se při sčítání vícemístných čísel přičítá, podobně jako při sčítání v desítkové soustavě, vždy k následujícímu sloupci sčítanců.
| Příklad: | 4 | = | 100 | 1 | = | 1 | = | 001 | |
| +5 | = | 101 | +5 | = | 101 | = | 101 | ||
| 9 | = | 1001 | 6 | = | = | 110 |
|
1 1 |
2 10 |
3 11 |
4 100 |
5 101 |
6 110 |
7 111 |
8 1000 |
9 1001 |
10 1010 |
|
11 1011 |
12 1100 |
13 1101 |
14 1110 |
15 1111 |
16 10000 |
17 10001 |
18 10010 |
19 10011 |
20 10100 |
Římské číslice
V minulých dobách se k zapisování čísel používaly běžně římské číslice, jejichž přehled je uveden v tabulce.
Číslo zapsané římskými číslicemi přečteme tak, že sečteme čísla zapsaná jednotlivými číslicemi:
Příklad: III = 3 XII = 12 MDCCCLXVII = 1867
Jestliže v zápisu čísla předchází menší číslice před větší číslicí, pak se menší číslice od větší číslice odečítá.
Příklad: IV = 4 MCM = 1900 MCMLXXXIV = 1984
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
50 |
100 |
500 |
1000 |
XXI = 21 CV = 105 |
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
L |
C |
D |
M |
MDCLXVI = |
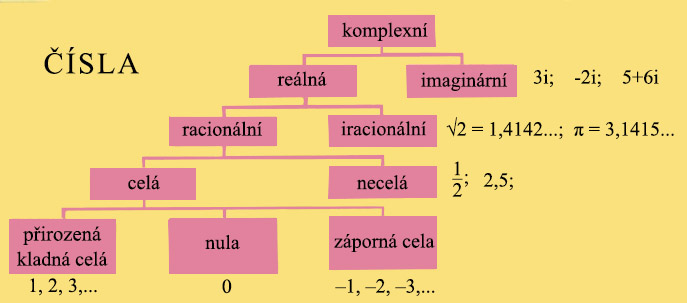
Množiny čísel
Rozdělení množin čísel je uvedeno v tabulce.
Přirozená čísla neboli kladná celá čísla 1,2,3, ... jsou čísla, jimiž vyjadřujeme počet předmětů, věcí, osob apod. Někdy k přirozeným číslům řadíme i číslo 0 a takto chápaná množina přirozených čísel se nazývá množina nezáporných celých čísel.
Celá čísla jsou tvořena množinou všech kladných celých čísel 1, 2, 3, ..., množinou všech záporných celých čísel -1, -2, -3, ... a číslem 0.
Racionální čísla jsou čísla, která lze zapsat ve tvaru 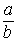 , kde a, b jsou celá čísla, přičemž b je kladné.
, kde a, b jsou celá čísla, přičemž b je kladné.
Iracionální čísla jsou například čísla √2 = 1,41421 ..., nebo Ludolfovo číslo π = 3,141 59 ... a další, která nelze zapsat ve tvaru zlomku jako racionální čísla.
Reálná čísla jsou tvořena množinou racionálních čísel a množinou iracionálních čísel. Reálné číslo, které je záporné nebo rovno nule, se nazývá nekladné číslo. Reálné číslo, které je kladné nebo rovno nule, se nazývá nezáporné číslo. Znaménko + se u kladných reálných čísel obvykle vynechává a místo + 5, + 3,5 píšeme 5, 3,5. Množiny čísel označujeme zpravidla těmito písmeny:
N — přirozená čísla R — reálná čísla
Z — celá čísla C — komplexní čísla
Q — racionální čísla
a dale například R+ — kladna čísla
Q — záporná racionální čísla.
Dělitelnost čísel
Dělíme-li celé kladné číslo a celým kladným číslem b a dělení vyjde beze zbytku, říkáme, že „číslo a je dělitelné číslem b“ nebo „číslo b je dělitelem čísla a“. Dělitelnost čísel zjišťujeme dělením nebo v jednoduchých případech podle znaků dělitelnosti:
- Číslo je dělitelné dvěma, končí-li jednou z číslic 0, 2, 4, 6, 8.
- Číslo je dělitelné třemi, je-li jeho ciferný součet (součet všech cifer, kterými je dané číslo zapsáno) dělitelný třemi.
- Číslo je dělitelné čtyřmi, je-li jeho poslední dvojčíslí dělitelné čtyřmi, nebo je-li ukončeno dvojčíslím 00.
- Číslo je dělitelné pěti, je-li ukončeno číslicí 0 nebo 5.
- Číslo je dělitelné šesti, je-li sudé a jeho ciferný součet je dělitelný třemi.
- Číslo je dělitelné osmi, je-li jeho poslední trojčíslí dělitelné osmi, nebo je-li ukončeno trojčíslím 000.
- Číslo je dělitelné devíti, je-li jeho ciferný součet dělitelný devíti.
- Číslo je dělitelné desíti, je-li ukončeno číslicí nula.
Prvočísla
Prvočísla jsou přirozená čísla dělitelná jen číslem 1 a sama sebou. Číslo 5 je prvočíslo, protože je dělitelné jen číslem 1 a číslem 5. Prvočísla menší než 100:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
K vyhledávání přirozených čísel můžeme použít postup zvaný Eratosthenovo síto. Máme-li vyhledat například všechna prvočísla menší než přirozené číslo n = 24, přeškrtneme číslo 1 (sledujte výklad na obrázku), které prvočíslem není, a pak postupně všechny vyšší násobky nejmenšího nepřeškrtnutého čísla, tedy postupně nejdříve vyšší násobky čísla 2 (= 4, 6, 8 ...), pak vyšší násobky dalšího nejmenšího nepřeškrtnutého čísla 3 (= 6, 9, 12 ...) atd. Hledaná prvočísla jsou ta čísla, která nejsou přeškrtnuta, tedy čísla 2, 3, 5, 7, 11, 13, 17, 19 a 23.

Složená čísla
Složená čísla jsou přirozená čísla, která mají alespoň tři dělitele. Číslo 9 je číslo složené, protože je kromě čísel 1 a 9 dělitelné také číslem 3. Číslo 1 není ani prvočíslo, ani číslo složené, protože má jen jediného dělitele, a to samo sebe.
Každé složené přirozené číslo lze zapsat jako součin dvou nebo více prvočísel, a to vždy (pokud nepřihlížíme k pořadí činitelů) jen jediným způsobem.
Příklad: 60 = 2·2·3·5
Rozklad čísla v součin prvočísel zjišťujeme u menších čísel úsudkem, u větších čísel postupným dělením daného čísla a vypočtených podílů prvočísly od nejmenšího k vyššímu, až je podíl roven jedné.
Příklad: 60:2 = 30 30:2 = 15
15:3 = 5 5:5 = 1 60 = 2·2·3·5
Společný dělitel dvou nebo více přirozených čísel je přirozené číslo, které je dělitelem každého z nich.
Příklad: Čísla 18 a 30 mají dělitele
18: 1, 2, 3, 6, 9, 18
30: 1, 2, 3, 5, 6, 10, 15, 30.
Společní dělitelé čísel 18 a 30 jsou čísla 1, 2, 3 a 6.
Největší společný dělitel čísel a, b, c, ... se označuje D (a,b,c,...) a vypočte tak, že daná čísla rozložíme v součin prvočísel, podškrtneme všechna prvočísla, která se vyskytují současně ve vše'ch rozkladech, a podškrtnutá čísla znásobíme.
Příklad: Největšího společného dělitele čísel 54 a 360 vypočteme po rozkladu v součin prvočísel
54 = 2 · 3 · 3 · 3
360 = 2 · 2 · 2 · 3 · 3 · 5
znásobením podškrtnutých prvočísel v prvním nebo druhém rozkladu
D (54, 360) = 2·3·3 = 18
Společný násobek dvou nebo více přirozených čísel je přirozené číslo, které je celistvým násobkem každého z nich.
| Příklad: | Násobky čísel 3 a 4 jsou čísla 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, ... 4: 4, 8, 12, 16, 20, 24, 28, 32, ... Společné násobky čísel 3 a 4 jsou čísla 12, 24, ... |
Nejmenší společný násobek čísel a, b, c se označuje n (a, b. c, ...) a vypočte tak, že daná čísla rozložíme v součin prvočísel, podškrtneme všechna různá prvočísla vždy v největším počtu, v němž se v některém rozkladu vyskytnou, a podškrtnutá čísla znásobíme.
Příklad: Nejmenší společný násobek čísel 12 a 90 vypočteme po rozkladu v součin prvočísel
12 = 2 · 2 · 3
90 = 2 · 3 · 3 · 5
znásobením podškrtnutých prvočísel n (12, 90) = 2 · 2 · 3 · 3 · 5 = 180.
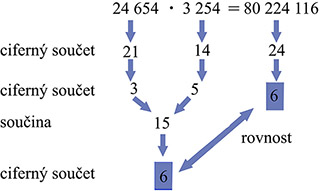
Devítková zkouška
O správnosti násobení nebo dělení se můžeme přesvědčit devítkovou zkouškou, znázorněnou na schématu. Ciferný součet je součet čísel vyjádřených jeho číslicemi, například ciferný součet čísla 24 654 je 2 + 4 + 6 + 5 + 4 = 21. Jestliže se devítkovou zkouškou vypočtená čísla rovnají, lze předpokládat, že je výsledek násobení správný (ve výjimečných případech vyjde rovnost i při nesprávném výsledku násobení), jestliže se nerovnají, je výsledek násobení jistě chybný.