MATEMATICKÉ ZNAČKY
Všeobecné značky
1,2, . . ., n
konečná posloupnost čísel od
1 do n
1, 2, 3, . . .
nekonečná posloupnost čísel
a1, a2 . . .
rozlišení čísel s indexy i = 1, 2, . . .
Aritmetika a algebra
a = b
a se rovná b, rovnítko
a ≠ b
a se nerovná b
a > b
a je větší než b (ostrá nerovnost)
a < b
a je menší než b (ostrá nerovnost)
a ≧ b
a je větší nebo rovno b (neostrá nerovnost)
a ≦ b
a je menší nebo rovno b (neostrá nerovnost)
a ≐ b
a se rovná přibližně b
a < x < b
a je menší než x je menší než b
(a, b)
otevřený interval a < x < b
⟨a, b⟩
uzavřený interval a ≦ x ≦ b
a + b
a plus b, sčítání (kladné znaménko)
a – b
a minus b, odčítání (záporné znaménko)
a · b
a krát b, násobení
| a : b, | a |
| b |
a děleno, lomeno b, dělení, zlomková čára
an
ntá mocnina a, umocňování
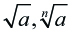
druhá, ntá odmocnina a, odmocňování, odmocnítko
|a|
absolutní hodnota
a%
a procent (= jedna setina a)
a‰
a promile (= jedna tisícina a)
( ), [ ], { }
závorka okrouhlá, lomená, složená
logax
logaritmus x při základu a
log x, lg x
logaritmus x při základu 10
ln x
přirozený logaritmus x (loge x)
Množiny
{a, b, c}
množina prvků a, b, c
a ∈ M
a je prvkem množiny M
a ∉ M
a není prvkem množiny M, a ne patří do M
∅
prázdná množina
A ⋃ B
sjednocení množin A, B
A ⋂ B
průnik množin A, B
A \ B
rozdíl množin A, B
A = B, A ≠ B
rovnost, nerovnost množin A, B
A ⊂ B
množina A je podmnožinou množiny B, inkluze
Geometrie
a || b
přímka a je rovnoběžná s přímkou b
a ⟂ b
přímka a je kolmá k přímce b
a ≠ b
přímky a, b jsou různé, nesplývají
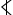 AVB
AVB
konvexní úhel s vrcholem V
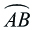
oblouk křivky s krajními body A, B
∆ ABC
trojúhelník s vrcholy A, B, C
≅
znak shodnosti, například ∆ ABC ≅ ∆ A´B´C´
sin x
sinus x
cos x
kosinus x
tg x
tangens x
cotg x
kotangens x
Konstanty a symboly
π
Ludolfovo číslo π ≐ 3,141 59...
e
základ přirozených logaritmů e = 2,718 28 ...
i
imaginární jednotka, i2 = -1